The goal of this project was to solve the Cart Pole problem from the Python OpenAI Gym library. The goal of the Cart Pole problem is to balance a pole on a cart that runs on a frictionless rail. The cart can only be affected by a push left (action 0) or a push right (action 1).
This project uses Q-Learning to create a model that can be used to solve the problem. The created model can balance the pole upright without tipping or going offscreen. The model first puts the possible values of the observation space onto a discrete range so that Q-Values can be saved in a finite number of states. This also means that a relatively small number of states are needed since many values can be assigned to one state. Q-Values used to find the predicted best action to take based on the current state. Q-Values are associated with a specific state and action. A higher Q-Value means the action has a higher chance to succeed based on observed rewards. These values are calculated based on the following formula.
The formula uses the saved Q-Values at the current and next state to calculate the new value. The reward is given by the OpenAI Gym environment based on whether the action succeded or not. The formula also contains two parameters: alpha and gamma. Alpha is the rate at which the Q-Value changes based on the reward. In my project, alpha is initially set to 0.5, but changes to 0.1 after 225 episodes. This means that earlier actions are more infuential on the learning. The model changes less as time goes on. Gamma is the discount factor, meaning it determines how much the predicted value is used in the calculation of the new value. In my project, gamma is kept as a constant 1 to reinforce the model.
Another parameter unseen in the formula is epsilon. This is also known as the exploration rate and determines how often random actions are taken. In my program, epsilon is initially set to 1, but, like alhpa, changes to .1 after 225 episodes. This means it will take completely random actions for the first 225 episodes in order to teach the model. After the 225 episodes, it will be less likely that a random action is taken so that the model can be reinforced.
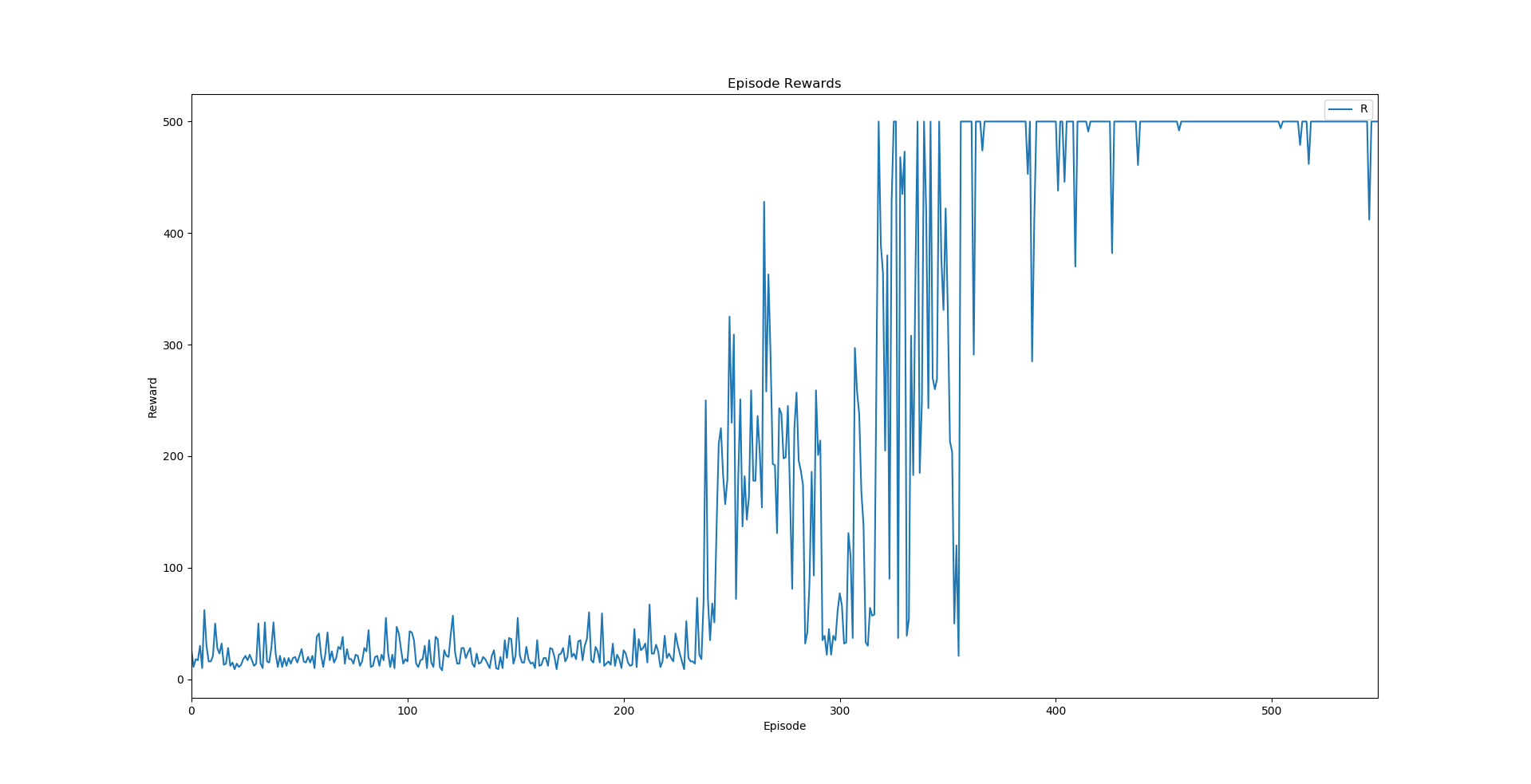
A line graph of the rewards at each episode is shown below. This graph was generated using a tool I created. The rewards are low for the first 225 episodes, where random actions were taken. After the model begins predicting the next action, the reward values are much higher. By the 400th episode, the model consistently gets rewards above 300 and frequently at the maximum value of 500.
